|
|
|
Fernando Peruani
Research:
This is an outdated description of my research activities, but it still provides an idea of the topics I am interested in.
Active matter - Physics of biological systems
Self-propelled Particles (SPPs) with Nematic Interactions: From Simple Agent-Based Models to Experiments with Myxobacteria
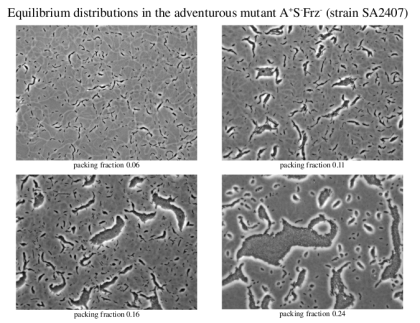 Myxobacteria are gram-negative rod-shaped bacteria that move by gliding, i.e., they do not swim but glide on surfaces.
Bacterial gliding is a process that does not involve the use of flagella. In Myxococcus xanthus is it believed that self-propulsion is achieved by either the secretion of a polysaccharide slime from nozzles at either end of the body, or by the use of an contractile appendage called type IV pili at one of the end of the bacterium.
If these bacteria sense a severe depletion of nutrients, they undergo a transition to multicellularity that culminates in what is called fruiting-body formation.
How these bacteria coordinate their motion is an open question. It is known that myxobacteria communicate through a signaling mechanisms called C-signal, which requires cell-to-cell contact in order to be transmitted. C-signal controls the reversal frequency of the wild-type myxobacteria, which perform a back-and-forth movement. The transition is known to occur when the frequency tends to zero.
But still, how does a group of cell manage to migrate coherently in the same direction? What kind of orientational information do these cells exchange? How can they reach concensus to decide in which direction migrate?
We found a simple explanation to these puzzling questions. Myxobacteria exchange orientational information in the form of forces and torques.
Myxobacteria are gram-negative rod-shaped bacteria that move by gliding, i.e., they do not swim but glide on surfaces.
Bacterial gliding is a process that does not involve the use of flagella. In Myxococcus xanthus is it believed that self-propulsion is achieved by either the secretion of a polysaccharide slime from nozzles at either end of the body, or by the use of an contractile appendage called type IV pili at one of the end of the bacterium.
If these bacteria sense a severe depletion of nutrients, they undergo a transition to multicellularity that culminates in what is called fruiting-body formation.
How these bacteria coordinate their motion is an open question. It is known that myxobacteria communicate through a signaling mechanisms called C-signal, which requires cell-to-cell contact in order to be transmitted. C-signal controls the reversal frequency of the wild-type myxobacteria, which perform a back-and-forth movement. The transition is known to occur when the frequency tends to zero.
But still, how does a group of cell manage to migrate coherently in the same direction? What kind of orientational information do these cells exchange? How can they reach concensus to decide in which direction migrate?
We found a simple explanation to these puzzling questions. Myxobacteria exchange orientational information in the form of forces and torques.
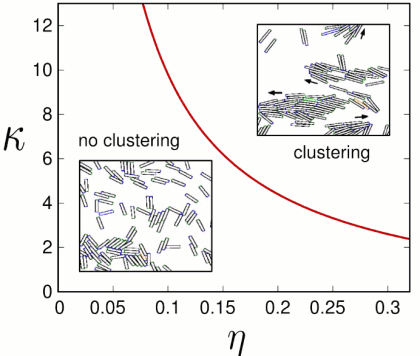 We have shown that the elongated rod shape of bacteria plays a central role in their collective motion. Moreover, for a given density η there is a critical aspect κ above which there is a transition to clustering (=collective migration). To show that, we described myxobacteria as simple self-propelled rods that interact only by volume exclusion.
We have shown that the elongated rod shape of bacteria plays a central role in their collective motion. Moreover, for a given density η there is a critical aspect κ above which there is a transition to clustering (=collective migration). To show that, we described myxobacteria as simple self-propelled rods that interact only by volume exclusion.
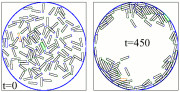 We studied this system by performing extensive individual-based simulations, and analytically by deriving a clustering theory for this system.
We have applied this self-propelled rod approach to study the collective behavior of a particular Myxococcus xanthus mutant, the adventurous A+S-Frz- mutant which do not reverse but still exhibits a rich collective dynamics.
For more detail see: [M1]
[M2]
We studied this system by performing extensive individual-based simulations, and analytically by deriving a clustering theory for this system.
We have applied this self-propelled rod approach to study the collective behavior of a particular Myxococcus xanthus mutant, the adventurous A+S-Frz- mutant which do not reverse but still exhibits a rich collective dynamics.
For more detail see: [M1]
[M2]
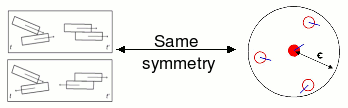
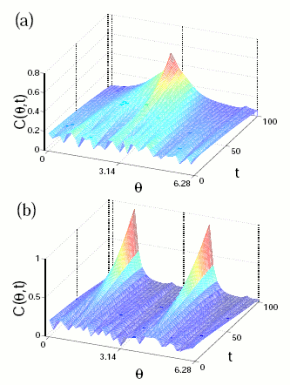 Self-propelled rods are polar particles, since as being self-propelled, we can differentiate "head" and "tail". Their interactions, however, are due exclusively to volume exclusion and in consequence are apolar, as in liquid -crystals.
So, a system of self-propelled rods is a system of polar particles with apolar interactions.
It is well known that a two-dimensional system of polar particles with polar interactions exhibits a transition to global polar order characterized by the emergence of true long-range order. This means that if initially the particles in the system point with equal probability in any direction and the noise is low enough, the system evolves towards an state where there is only one direction available in the system.
On the other hand, it is also known that a two-dimensional system of driven apolar particles with apolar interactions, as shaken grains, cannot evolve towards an state with orientational order. In this case, the system is known to display a Kosterlitz-Thouless transition with quasi-long range order. A system of self-propelled rods, as myxobacteria, is a mixed case of, as said above, polar particles with apolar interactions. So, what is going to happen in this system? Does the system develop some sort of orientational order? Is that order polar or apolar? What kind of phase transition does the system exhibit? We have been working on these questions and we can already give some answers. If we prepare two systems that are identical in everything (density, noise level, etc) except for the symmetry of the interactions, we have been able to show theoretically (and by simulations) that the system with apolar interactions evolves towards an ordered state characterized by the presence of two opposite directions available in the system (apolar order). Moreover, the transition for this system occurs for lower noise values than for the system with polar interactions. Furthermore, the system seems to be able to develop long-range order and the transition seems to be first order. For more detail see:[R1]
[R2]
Self-propelled rods are polar particles, since as being self-propelled, we can differentiate "head" and "tail". Their interactions, however, are due exclusively to volume exclusion and in consequence are apolar, as in liquid -crystals.
So, a system of self-propelled rods is a system of polar particles with apolar interactions.
It is well known that a two-dimensional system of polar particles with polar interactions exhibits a transition to global polar order characterized by the emergence of true long-range order. This means that if initially the particles in the system point with equal probability in any direction and the noise is low enough, the system evolves towards an state where there is only one direction available in the system.
On the other hand, it is also known that a two-dimensional system of driven apolar particles with apolar interactions, as shaken grains, cannot evolve towards an state with orientational order. In this case, the system is known to display a Kosterlitz-Thouless transition with quasi-long range order. A system of self-propelled rods, as myxobacteria, is a mixed case of, as said above, polar particles with apolar interactions. So, what is going to happen in this system? Does the system develop some sort of orientational order? Is that order polar or apolar? What kind of phase transition does the system exhibit? We have been working on these questions and we can already give some answers. If we prepare two systems that are identical in everything (density, noise level, etc) except for the symmetry of the interactions, we have been able to show theoretically (and by simulations) that the system with apolar interactions evolves towards an ordered state characterized by the presence of two opposite directions available in the system (apolar order). Moreover, the transition for this system occurs for lower noise values than for the system with polar interactions. Furthermore, the system seems to be able to develop long-range order and the transition seems to be first order. For more detail see:[R1]
[R2]
Random Walks (SPPs) with Fluctuations in the Direction of Motion and in the Speed
 Let us make an analogy between a random walker and a car.
Imagine you drive a car in a huge empty park at constant speed while randomly turning the direction wheel.
What kind of motion do you perform? The answer is simple, you perform what is called a persistent Brownian motion.
Imagine now something slightly different.
Let us make an analogy between a random walker and a car.
Imagine you drive a car in a huge empty park at constant speed while randomly turning the direction wheel.
What kind of motion do you perform? The answer is simple, you perform what is called a persistent Brownian motion.
Imagine now something slightly different.
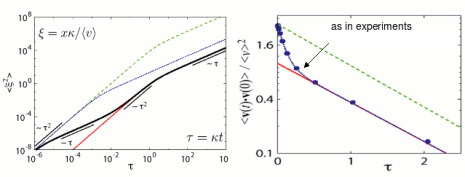 If instead of keeping the speed constant, you randomly press the gas and break pedals, while still randomly turning the direction wheel, your resulting movement is no longer well described as a simple persistent Brownian motion. The statistics of the movement has changed.
We have recently addressed this problem and focused on the new features introduced by the fluctuations in the speed. In particular, we have shown that there is a complex transient, together with changes in the asymptotic properties of the movement due to the speed fluctuations. Our results are relevant to understand the motion of small self-propelled particles subject to large fluctuations in their motion. We suggest that some recent cell motility experiments, which exhibit important fluctuations in the speed and the direction of motion, could be described in terms of a simple random walk with fluctuations in the direction of motion and in the speed. For more details see [RW1].
If instead of keeping the speed constant, you randomly press the gas and break pedals, while still randomly turning the direction wheel, your resulting movement is no longer well described as a simple persistent Brownian motion. The statistics of the movement has changed.
We have recently addressed this problem and focused on the new features introduced by the fluctuations in the speed. In particular, we have shown that there is a complex transient, together with changes in the asymptotic properties of the movement due to the speed fluctuations. Our results are relevant to understand the motion of small self-propelled particles subject to large fluctuations in their motion. We suggest that some recent cell motility experiments, which exhibit important fluctuations in the speed and the direction of motion, could be described in terms of a simple random walk with fluctuations in the direction of motion and in the speed. For more details see [RW1].
Information/Disease Spreading in Moving Agent Systems
The understanding of information propagation through a system of moving agents is crucial for many applications, ranging from chemical reactions to epidemic spreading. Depending on the context, the information that is transferred can take the form of an excitation, in chemical reaction, a disease, in epidemics, or more explicitly, information packages, in peer-to-peer telephony. One fundamental questions is whether the information will disappear from the system after a finite time or whether the system is robust enough to maintain indefinitely a fraction of informed agents. In other words, our main goal is to understand the broadcasting and routing properties of moving agent systems, that are encoded in the steady states of such system, which strongly depend on the motility pattern exhibited by the agents.
Traditionally, the study of either disease or information spreading have been performed on either a lattice, a network, or directly using a mean-field.
The correlation among the agents/nodes differ dramatically in all these three cases, and consequently the information spreading dynamics also displays important differences. Moving agent systems appears, in consequence, as a fourth "platform" to study information spreading.
However, we have shown that a moving agent system, where the information transfer requires agents to keep physical contact for a non-vanishing time, while interacting in space by volume exclusion, bridges the gap between the three mentioned cases: lattice, complex network, and mean-field models.
For instance, at high density, our agents can hardly move and the information spreading dynamics resembles that of a lattice. At intermediate densities, the system exhibits a complex networks-like behavior, while at low density the information spreading dynamics is mean-field.
Our moving agent model has allowed us to put into the same theoretical framework lattice, network, and mean-field approaches.
In addition to that, we have focused on the role of the agent active speed v. In particular, we have shown that there exist three regimes with v: "information extinction" for small v, an "endemic" regime in which the number of non-informed agents is inversely proportional to v, and a third regime, model dependent, for large v, proportional to v to the power A-1, where A is the scaling exponent of the mean collision time with v. We have recently applied these results to estimate the mean broadcasting time (=time required to inform all agents in the system) and the mean routing time in ad hoc networks of moving agents. For more details see: [E1][E2].
HIV infection dynamics
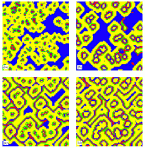 The spread of the HIV infection among target cells in lymphoid tissues can be qualitatively described by a cellular automata model (Phys. Rev. Lett. 87, 168102 (2001)).
We have investigated the robustness of this model against various parameter changes.
We have observed that an increase of the cell resistance, at any
stage of the infection, leads to a reduction of the latency period, i.e., of the time interval
between the primary infection and the onset of AIDS.
We also extended the model to include inhomogeneities on the cells properties, as for instance,
on the cell resistance or on the time interval to mount specific immune responses. For more details see: [H1].
The spread of the HIV infection among target cells in lymphoid tissues can be qualitatively described by a cellular automata model (Phys. Rev. Lett. 87, 168102 (2001)).
We have investigated the robustness of this model against various parameter changes.
We have observed that an increase of the cell resistance, at any
stage of the infection, leads to a reduction of the latency period, i.e., of the time interval
between the primary infection and the onset of AIDS.
We also extended the model to include inhomogeneities on the cells properties, as for instance,
on the cell resistance or on the time interval to mount specific immune responses. For more details see: [H1].
Complex Networks
Alphabetic Bipartite Networks - understanding codon usage
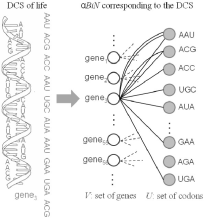 Life and language are discrete combinatorial systems (DCSs) in
which the basic building blocks are finite sets of elementary units:
nucleotides or codons, in a DNA sequence, and letters or words, in a language.
Different combinations of these finite units give rise to
potentially infinite numbers of genes or sentences. This type of
DCS can be represented by what we have called Alphabetic Bipartite Network
(α-BiN) .
Life and language are discrete combinatorial systems (DCSs) in
which the basic building blocks are finite sets of elementary units:
nucleotides or codons, in a DNA sequence, and letters or words, in a language.
Different combinations of these finite units give rise to
potentially infinite numbers of genes or sentences. This type of
DCS can be represented by what we have called Alphabetic Bipartite Network
(α-BiN) .
 In α-BiNs, there are two kinds of nodes, one type represents the elementary units
while the other type represents their combinations. There is an edge between a node
corresponding to an elementary unit u and a node corresponding to
a particular combination v if u is present in v.
Naturally, the partition
consisting of the nodes representing elementary units is fixed,
while the other partition is allowed to grow unboundedly.
We have derived several analytical results for α-BiNs and the associated one-mode projection, under different growth rules.
In particular, we have shown that asymptotically the degree distribution of α-BiNs can be described as a family of beta
distributions.
We have applied these analytical findings to real world systems,
the codon-gene network and the phoneme-language network, as a means for inferring the mechanisms
underlying the growth of real world systems.
Our work suggests that statistics on codon usage can be helpful to classify organisms, in particularly
when genome sequences are only available in fragments either due to fragmentary sampling of the biological
material or to un-finished sequencing efforts. For more details see: [A1][A2].
In α-BiNs, there are two kinds of nodes, one type represents the elementary units
while the other type represents their combinations. There is an edge between a node
corresponding to an elementary unit u and a node corresponding to
a particular combination v if u is present in v.
Naturally, the partition
consisting of the nodes representing elementary units is fixed,
while the other partition is allowed to grow unboundedly.
We have derived several analytical results for α-BiNs and the associated one-mode projection, under different growth rules.
In particular, we have shown that asymptotically the degree distribution of α-BiNs can be described as a family of beta
distributions.
We have applied these analytical findings to real world systems,
the codon-gene network and the phoneme-language network, as a means for inferring the mechanisms
underlying the growth of real world systems.
Our work suggests that statistics on codon usage can be helpful to classify organisms, in particularly
when genome sequences are only available in fragments either due to fragmentary sampling of the biological
material or to un-finished sequencing efforts. For more details see: [A1][A2].
Stability of Finite Complex Network and Peer-to-Peer Networks
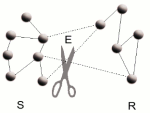 Though many results have been derived for infinite scale-free (SF) networks, very little is known about the stability of finite networks.
Typical examples of small size finite networks are ad-hoc networks of commercial mobile devices, frequently used in communication,
and networks of autonomous mobile robots.
The operation of these systems rely on the robustness of the highly dynamical underlying network.
Thus, a good understanding on the stability of these small size networks is imperative for these applications.
Moreover, we can say that in general a comprehensive theory for the stability of arbitrary finite networks under any node disturbance is still lacking.
We have attempted to shed some light on this matter by proposing an alternative derivation for the percolation threshold.
Instead of applying a generating function formalism to find an analytic expression for the percolation threshold, we used the fact that during an attack the degree distribution of the network changes.
We have shown that the degree distribution of the distorted (uncorrelated) network, under any node disturbances,
can be easily computed through a simple formula.
Though many results have been derived for infinite scale-free (SF) networks, very little is known about the stability of finite networks.
Typical examples of small size finite networks are ad-hoc networks of commercial mobile devices, frequently used in communication,
and networks of autonomous mobile robots.
The operation of these systems rely on the robustness of the highly dynamical underlying network.
Thus, a good understanding on the stability of these small size networks is imperative for these applications.
Moreover, we can say that in general a comprehensive theory for the stability of arbitrary finite networks under any node disturbance is still lacking.
We have attempted to shed some light on this matter by proposing an alternative derivation for the percolation threshold.
Instead of applying a generating function formalism to find an analytic expression for the percolation threshold, we used the fact that during an attack the degree distribution of the network changes.
We have shown that the degree distribution of the distorted (uncorrelated) network, under any node disturbances,
can be easily computed through a simple formula.
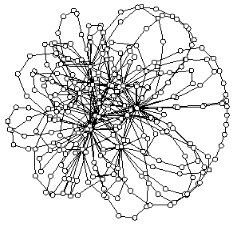 Based on this expression, we have derived a general condition for the stability of non-correlated complex networks under any arbitrary attack.
This condition applied to the study of network stability under a general attack of the form f(k) ∼ k^γ, where f(k) stands for the probability of a node of degree k of being removed
during the attack, leads us to a general expression for the percolation threshold fc.
We have shown that fc of a finite network of size N exhibits an additive correction
which scales as N^(-1) with respect to the classical result for infinite networks. For more details see: [S1] [S2].
Based on this expression, we have derived a general condition for the stability of non-correlated complex networks under any arbitrary attack.
This condition applied to the study of network stability under a general attack of the form f(k) ∼ k^γ, where f(k) stands for the probability of a node of degree k of being removed
during the attack, leads us to a general expression for the percolation threshold fc.
We have shown that fc of a finite network of size N exhibits an additive correction
which scales as N^(-1) with respect to the classical result for infinite networks. For more details see: [S1] [S2].
We have also focused on the stability of a type of technological networks that are particularly challenging: peer-to-peer (p2p) networks. Users of peer-to-peer system join and leave the network constantly, which
makes the overlay network dynamics of such systems very unstable in nature. We have proposed an
analytical framework to assess the robustness of p2p networks in the face of user churn.
We have modeled the peer churn through degree-independent as well as degree-dependent node
failure. We have also considered system with superpeer nodes, since these systems are becoming the most widely used topology among
the p2p networks. We have shown that a small fraction of superpeers can improve remarkably the robustness of the network.
For more details see:
[Pr1]
[Pr2]
[Pr3]
Dielectric Breakdown
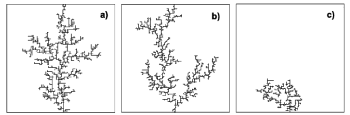 We have generalized the classical dielectric breakdown
model to describe dielectric breakdown patterns in either conductor-loaded or isolator-loaded composites. The impurities are distributed at random in the dielectric matrix. The breakdown of the material propagates according
to new rules. The obtained dielectric breakdown patterns were
characterized by their fractal dimension D and the parameters of the Weibull distribution. For more details see:
[D1][D2]
We have generalized the classical dielectric breakdown
model to describe dielectric breakdown patterns in either conductor-loaded or isolator-loaded composites. The impurities are distributed at random in the dielectric matrix. The breakdown of the material propagates according
to new rules. The obtained dielectric breakdown patterns were
characterized by their fractal dimension D and the parameters of the Weibull distribution. For more details see:
[D1][D2]
|

 Myxobacteria are gram-negative rod-shaped bacteria that move by gliding, i.e., they do not swim but glide on surfaces.
Bacterial gliding is a process that does not involve the use of flagella. In Myxococcus xanthus is it believed that self-propulsion is achieved by either the secretion of a polysaccharide slime from nozzles at either end of the body, or by the use of an contractile appendage called type IV pili at one of the end of the bacterium.
If these bacteria sense a severe depletion of nutrients, they undergo a transition to multicellularity that culminates in what is called fruiting-body formation.
How these bacteria coordinate their motion is an open question. It is known that myxobacteria communicate through a signaling mechanisms called C-signal, which requires cell-to-cell contact in order to be transmitted. C-signal controls the reversal frequency of the wild-type myxobacteria, which perform a back-and-forth movement. The transition is known to occur when the frequency tends to zero.
But still, how does a group of cell manage to migrate coherently in the same direction? What kind of orientational information do these cells exchange? How can they reach concensus to decide in which direction migrate?
We found a simple explanation to these puzzling questions. Myxobacteria exchange orientational information in the form of forces and torques.
Myxobacteria are gram-negative rod-shaped bacteria that move by gliding, i.e., they do not swim but glide on surfaces.
Bacterial gliding is a process that does not involve the use of flagella. In Myxococcus xanthus is it believed that self-propulsion is achieved by either the secretion of a polysaccharide slime from nozzles at either end of the body, or by the use of an contractile appendage called type IV pili at one of the end of the bacterium.
If these bacteria sense a severe depletion of nutrients, they undergo a transition to multicellularity that culminates in what is called fruiting-body formation.
How these bacteria coordinate their motion is an open question. It is known that myxobacteria communicate through a signaling mechanisms called C-signal, which requires cell-to-cell contact in order to be transmitted. C-signal controls the reversal frequency of the wild-type myxobacteria, which perform a back-and-forth movement. The transition is known to occur when the frequency tends to zero.
But still, how does a group of cell manage to migrate coherently in the same direction? What kind of orientational information do these cells exchange? How can they reach concensus to decide in which direction migrate?
We found a simple explanation to these puzzling questions. Myxobacteria exchange orientational information in the form of forces and torques.
 We have shown that the elongated rod shape of bacteria plays a central role in their collective motion. Moreover, for a given density η there is a critical aspect κ above which there is a transition to clustering (=collective migration). To show that, we described myxobacteria as simple self-propelled rods that interact only by volume exclusion.
We have shown that the elongated rod shape of bacteria plays a central role in their collective motion. Moreover, for a given density η there is a critical aspect κ above which there is a transition to clustering (=collective migration). To show that, we described myxobacteria as simple self-propelled rods that interact only by volume exclusion.
 We studied this system by performing extensive individual-based simulations, and analytically by deriving a clustering theory for this system.
We have applied this self-propelled rod approach to study the collective behavior of a particular Myxococcus xanthus mutant, the adventurous A+S-Frz- mutant which do not reverse but still exhibits a rich collective dynamics.
For more detail see: [
We studied this system by performing extensive individual-based simulations, and analytically by deriving a clustering theory for this system.
We have applied this self-propelled rod approach to study the collective behavior of a particular Myxococcus xanthus mutant, the adventurous A+S-Frz- mutant which do not reverse but still exhibits a rich collective dynamics.
For more detail see: [
 Self-propelled rods are polar particles, since as being self-propelled, we can differentiate "head" and "tail". Their interactions, however, are due exclusively to volume exclusion and in consequence are apolar, as in liquid -crystals.
So, a system of self-propelled rods is a system of polar particles with apolar interactions.
It is well known that a two-dimensional system of polar particles with polar interactions exhibits a transition to global polar order characterized by the emergence of true long-range order. This means that if initially the particles in the system point with equal probability in any direction and the noise is low enough, the system evolves towards an state where there is only one direction available in the system.
On the other hand, it is also known that a two-dimensional system of driven apolar particles with apolar interactions, as shaken grains, cannot evolve towards an state with orientational order. In this case, the system is known to display a Kosterlitz-Thouless transition with quasi-long range order. A system of self-propelled rods, as myxobacteria, is a mixed case of, as said above, polar particles with apolar interactions. So, what is going to happen in this system? Does the system develop some sort of orientational order? Is that order polar or apolar? What kind of phase transition does the system exhibit? We have been working on these questions and we can already give some answers. If we prepare two systems that are identical in everything (density, noise level, etc) except for the symmetry of the interactions, we have been able to show theoretically (and by simulations) that the system with apolar interactions evolves towards an ordered state characterized by the presence of two opposite directions available in the system (apolar order). Moreover, the transition for this system occurs for lower noise values than for the system with polar interactions. Furthermore, the system seems to be able to develop long-range order and the transition seems to be first order. For more detail see:[
Self-propelled rods are polar particles, since as being self-propelled, we can differentiate "head" and "tail". Their interactions, however, are due exclusively to volume exclusion and in consequence are apolar, as in liquid -crystals.
So, a system of self-propelled rods is a system of polar particles with apolar interactions.
It is well known that a two-dimensional system of polar particles with polar interactions exhibits a transition to global polar order characterized by the emergence of true long-range order. This means that if initially the particles in the system point with equal probability in any direction and the noise is low enough, the system evolves towards an state where there is only one direction available in the system.
On the other hand, it is also known that a two-dimensional system of driven apolar particles with apolar interactions, as shaken grains, cannot evolve towards an state with orientational order. In this case, the system is known to display a Kosterlitz-Thouless transition with quasi-long range order. A system of self-propelled rods, as myxobacteria, is a mixed case of, as said above, polar particles with apolar interactions. So, what is going to happen in this system? Does the system develop some sort of orientational order? Is that order polar or apolar? What kind of phase transition does the system exhibit? We have been working on these questions and we can already give some answers. If we prepare two systems that are identical in everything (density, noise level, etc) except for the symmetry of the interactions, we have been able to show theoretically (and by simulations) that the system with apolar interactions evolves towards an ordered state characterized by the presence of two opposite directions available in the system (apolar order). Moreover, the transition for this system occurs for lower noise values than for the system with polar interactions. Furthermore, the system seems to be able to develop long-range order and the transition seems to be first order. For more detail see:[ Let us make an analogy between a random walker and a car.
Imagine you drive a car in a huge empty park at constant speed while randomly turning the direction wheel.
What kind of motion do you perform? The answer is simple, you perform what is called a persistent Brownian motion.
Imagine now something slightly different.
Let us make an analogy between a random walker and a car.
Imagine you drive a car in a huge empty park at constant speed while randomly turning the direction wheel.
What kind of motion do you perform? The answer is simple, you perform what is called a persistent Brownian motion.
Imagine now something slightly different.
 If instead of keeping the speed constant, you randomly press the gas and break pedals, while still randomly turning the direction wheel, your resulting movement is no longer well described as a simple persistent Brownian motion. The statistics of the movement has changed.
We have recently addressed this problem and focused on the new features introduced by the fluctuations in the speed. In particular, we have shown that there is a complex transient, together with changes in the asymptotic properties of the movement due to the speed fluctuations. Our results are relevant to understand the motion of small self-propelled particles subject to large fluctuations in their motion. We suggest that some recent cell motility experiments, which exhibit important fluctuations in the speed and the direction of motion, could be described in terms of a simple random walk with fluctuations in the direction of motion and in the speed. For more details see [
If instead of keeping the speed constant, you randomly press the gas and break pedals, while still randomly turning the direction wheel, your resulting movement is no longer well described as a simple persistent Brownian motion. The statistics of the movement has changed.
We have recently addressed this problem and focused on the new features introduced by the fluctuations in the speed. In particular, we have shown that there is a complex transient, together with changes in the asymptotic properties of the movement due to the speed fluctuations. Our results are relevant to understand the motion of small self-propelled particles subject to large fluctuations in their motion. We suggest that some recent cell motility experiments, which exhibit important fluctuations in the speed and the direction of motion, could be described in terms of a simple random walk with fluctuations in the direction of motion and in the speed. For more details see [
 The spread of the HIV infection among target cells in lymphoid tissues can be qualitatively described by a cellular automata model (Phys. Rev. Lett. 87, 168102 (2001)).
We have investigated the robustness of this model against various parameter changes.
We have observed that an increase of the cell resistance, at any
stage of the infection, leads to a reduction of the latency period, i.e., of the time interval
between the primary infection and the onset of AIDS.
We also extended the model to include inhomogeneities on the cells properties, as for instance,
on the cell resistance or on the time interval to mount specific immune responses. For more details see: [
The spread of the HIV infection among target cells in lymphoid tissues can be qualitatively described by a cellular automata model (Phys. Rev. Lett. 87, 168102 (2001)).
We have investigated the robustness of this model against various parameter changes.
We have observed that an increase of the cell resistance, at any
stage of the infection, leads to a reduction of the latency period, i.e., of the time interval
between the primary infection and the onset of AIDS.
We also extended the model to include inhomogeneities on the cells properties, as for instance,
on the cell resistance or on the time interval to mount specific immune responses. For more details see: [ Life and language are discrete combinatorial systems (DCSs) in
which the basic building blocks are finite sets of elementary units:
nucleotides or codons, in a DNA sequence, and letters or words, in a language.
Different combinations of these finite units give rise to
potentially infinite numbers of genes or sentences. This type of
DCS can be represented by what we have called Alphabetic Bipartite Network
(α-BiN) .
Life and language are discrete combinatorial systems (DCSs) in
which the basic building blocks are finite sets of elementary units:
nucleotides or codons, in a DNA sequence, and letters or words, in a language.
Different combinations of these finite units give rise to
potentially infinite numbers of genes or sentences. This type of
DCS can be represented by what we have called Alphabetic Bipartite Network
(α-BiN) .
 In α-BiNs, there are two kinds of nodes, one type represents the elementary units
while the other type represents their combinations. There is an edge between a node
corresponding to an elementary unit u and a node corresponding to
a particular combination v if u is present in v.
Naturally, the partition
consisting of the nodes representing elementary units is fixed,
while the other partition is allowed to grow unboundedly.
We have derived several analytical results for α-BiNs and the associated one-mode projection, under different growth rules.
In particular, we have shown that asymptotically the degree distribution of α-BiNs can be described as a family of beta
distributions.
We have applied these analytical findings to real world systems,
the codon-gene network and the phoneme-language network, as a means for inferring the mechanisms
underlying the growth of real world systems.
Our work suggests that statistics on codon usage can be helpful to classify organisms, in particularly
when genome sequences are only available in fragments either due to fragmentary sampling of the biological
material or to un-finished sequencing efforts. For more details see: [
In α-BiNs, there are two kinds of nodes, one type represents the elementary units
while the other type represents their combinations. There is an edge between a node
corresponding to an elementary unit u and a node corresponding to
a particular combination v if u is present in v.
Naturally, the partition
consisting of the nodes representing elementary units is fixed,
while the other partition is allowed to grow unboundedly.
We have derived several analytical results for α-BiNs and the associated one-mode projection, under different growth rules.
In particular, we have shown that asymptotically the degree distribution of α-BiNs can be described as a family of beta
distributions.
We have applied these analytical findings to real world systems,
the codon-gene network and the phoneme-language network, as a means for inferring the mechanisms
underlying the growth of real world systems.
Our work suggests that statistics on codon usage can be helpful to classify organisms, in particularly
when genome sequences are only available in fragments either due to fragmentary sampling of the biological
material or to un-finished sequencing efforts. For more details see: [ Though many results have been derived for infinite scale-free (SF) networks, very little is known about the stability of finite networks.
Typical examples of small size finite networks are ad-hoc networks of commercial mobile devices, frequently used in communication,
and networks of autonomous mobile robots.
The operation of these systems rely on the robustness of the highly dynamical underlying network.
Thus, a good understanding on the stability of these small size networks is imperative for these applications.
Moreover, we can say that in general a comprehensive theory for the stability of arbitrary finite networks under any node disturbance is still lacking.
We have attempted to shed some light on this matter by proposing an alternative derivation for the percolation threshold.
Instead of applying a generating function formalism to find an analytic expression for the percolation threshold, we used the fact that during an attack the degree distribution of the network changes.
We have shown that the degree distribution of the distorted (uncorrelated) network, under any node disturbances,
can be easily computed through a simple formula.
Though many results have been derived for infinite scale-free (SF) networks, very little is known about the stability of finite networks.
Typical examples of small size finite networks are ad-hoc networks of commercial mobile devices, frequently used in communication,
and networks of autonomous mobile robots.
The operation of these systems rely on the robustness of the highly dynamical underlying network.
Thus, a good understanding on the stability of these small size networks is imperative for these applications.
Moreover, we can say that in general a comprehensive theory for the stability of arbitrary finite networks under any node disturbance is still lacking.
We have attempted to shed some light on this matter by proposing an alternative derivation for the percolation threshold.
Instead of applying a generating function formalism to find an analytic expression for the percolation threshold, we used the fact that during an attack the degree distribution of the network changes.
We have shown that the degree distribution of the distorted (uncorrelated) network, under any node disturbances,
can be easily computed through a simple formula.
 Based on this expression, we have derived a general condition for the stability of non-correlated complex networks under any arbitrary attack.
This condition applied to the study of network stability under a general attack of the form f(k) ∼ k^γ, where f(k) stands for the probability of a node of degree k of being removed
during the attack, leads us to a general expression for the percolation threshold fc.
We have shown that fc of a finite network of size N exhibits an additive correction
which scales as N^(-1) with respect to the classical result for infinite networks. For more details see: [
Based on this expression, we have derived a general condition for the stability of non-correlated complex networks under any arbitrary attack.
This condition applied to the study of network stability under a general attack of the form f(k) ∼ k^γ, where f(k) stands for the probability of a node of degree k of being removed
during the attack, leads us to a general expression for the percolation threshold fc.
We have shown that fc of a finite network of size N exhibits an additive correction
which scales as N^(-1) with respect to the classical result for infinite networks. For more details see: [ We have generalized the classical dielectric breakdown
model to describe dielectric breakdown patterns in either conductor-loaded or isolator-loaded composites. The impurities are distributed at random in the dielectric matrix. The breakdown of the material propagates according
to new rules. The obtained dielectric breakdown patterns were
characterized by their fractal dimension D and the parameters of the Weibull distribution. For more details see:
[
We have generalized the classical dielectric breakdown
model to describe dielectric breakdown patterns in either conductor-loaded or isolator-loaded composites. The impurities are distributed at random in the dielectric matrix. The breakdown of the material propagates according
to new rules. The obtained dielectric breakdown patterns were
characterized by their fractal dimension D and the parameters of the Weibull distribution. For more details see:
[