One-dimensional lattice gases and matrix-product states

Matrix-product states have recently turned out to be very useful for obtaining exact results on one-dimensional off-equilibrium lattice models. We are interested in applying this method to a broad range of models as well as in possible interrelations with other fields such as integrable models and the density-matrix renormalization group technique.

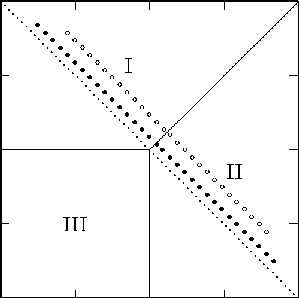
Concrete results have been obtained mainly for one model, namely the hopping motion of classical particles on a chain coupled to reservoirs at both ends with parallel dyanmics. It has turned out that there is a general relation of the parallel matrix-product algebra to that of the sequential limit. This can be used to generalize known results for sequential dynamics to the parallel case. In this manner we find the general phase diagram shown above.

This motion of classical particles can be mapped to a probably integrable asymmetric six-vertex model with boundaries.

If you would like to know more, take a look at our paper.

A supplementary program can be found here.

July, 29th, 1996

-- don't send me spam!