Form-factor bootstrap and the random-bond Ising model
Form-factor bootstrap and the random-bond Ising model
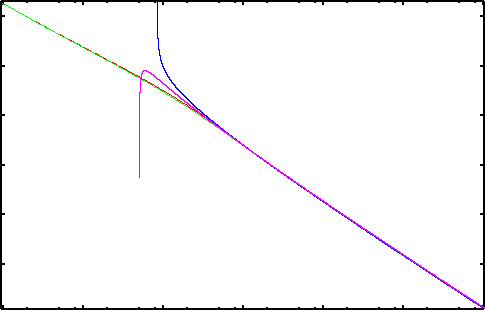
Two-point function of the energy operator
Disordered systems arise in generic situations where physical
systems are realized in nature. However, from a theoretical point of view
they represent a diffcult challenge. They can exhibit
complicated phenomena such as glassy behavior and logarithmic
corrections are abundant. Even numerical approaches are plagued
with the associated slow relaxation times or the necessity
of dealing with large system sizes.
In this context, the model we have concentrated on is the
two-dimensional Ising model with quenched random bonds. One
instance of this model with
two values of the coupling constant is illustrated by
this figure. In the scaling region of this lattice model
one can take the continuum limit and obtains Majorana fermions
with a random position-dependent mass term.
One is usually interested in quantities averaged over all possible
realizations of the randomness. A standard method to compute this
average e.g. of the free energy is the replica trick. If this
is applied to the aforementioned Majorana fermions with a random Gaussian
distributed mass term, the randomness can be integrated out.
This step leads to the O(N)-Gross-Neveu model which has been
already extensively studied within perturbative renormalization-group
approaches. However, this model happens to be integrabel and
one can obtain its exact S-matrix. Then one is in a position
to apply the form-factor approach to the computation of
correlation functions. Our main contribution has been to show
that this actually works and enables one to obtain valuable
non-perturbative information. The above figure
compares our result for the two-point function of the energy operator with
the one obtained in the perturbative framework.
If you would like to know more (details), you are invited to take
a look at this
paper.
May, 23th, 1997,
a.honecker@tu-bs.de
